MODEL
Sphere
AUTHOR/MODIFICATION
Steve Kline 06 NOV 1998
Alan Munter 08 JULY 1999, converted to Java
APPROVED FOR DISTRIBUTION
DESCRIPTION
Calculates the form factor, P(q), for a monodisperse spherical
particle with uniform scattering length density. The form factor is
normalized by the particle volume as described below.
Resolution smeared version is also provided.
VARIABLES
Input Variables (default values):
| Parameter | Variable | Value |
| 0 | Scale | 1.0 |
| 1 | Radius (Å) | 60.0 |
| 2 | Contrast (Å-2) | 1.0e-6 |
| 3 | Incoherent Background (cm-1) | 0.0 |
USAGE NOTES
The function calculated is:
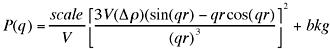
The returned value is scaled to units of [cm-1]
Scattering contrast (Dr) = SLD (core) - SLD (solvent)
Parameter[0] (scale) and Parameter[2] (contrast) are both
multiplicative factors in the model and are perfectly correlated. One
or both of these parameters must be held fixed during model fitting.
If the scale factor Parameter[0] is set equal to the particle
volume fraction, phi, then the returned value is the scattered
intensity per unit volume, I(q) = phi*P(q).
However, no interparticle interference effects are included in this
calculation.
REFERENCE
Guinier, A. and G. Fournet, "Small-Angle Scattering of X-Rays",
John Wiley and Sons, New York, (1955).
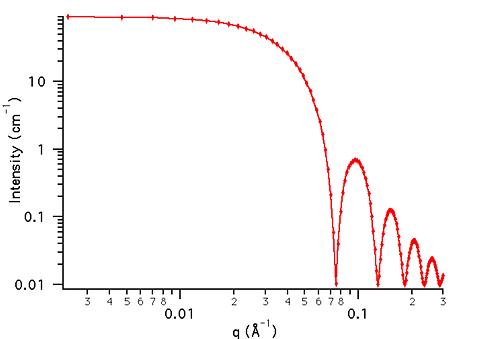
TEST DATASET
This example dataset is produced by calculating the Sphere using
128 data points, qmin = 0.001 Å-1,
qmax = 0.3 (Å-1) and the above default
parameter values.
![]()
